Draw a Circle From Three Points

To draw a direct line, the minimum number of points required is two. That means we can draw a straight line with the given two points. How many minimum points are sufficient to draw a unique circumvolve? Is it possible to draw a circumvolve passing through 3 points? In how many ways can we draw a circumvolve that passes through three points? Well, let's endeavor to discover answers to all these queries.

Learn: Circle Definition

Before drawing a circle passing through 3 points, permit'due south have a look at the circles that have been drawn through one and 2 points respectively.

Circle Passing Through a Bespeak

Let us consider a point and try to depict a circle passing through that bespeak.

As given in the figure, through a single betoken P, we can draw infinite circles passing through it.

Circle Passing Through Ii Points

Now, let us take ii points, P and Q and see what happens?

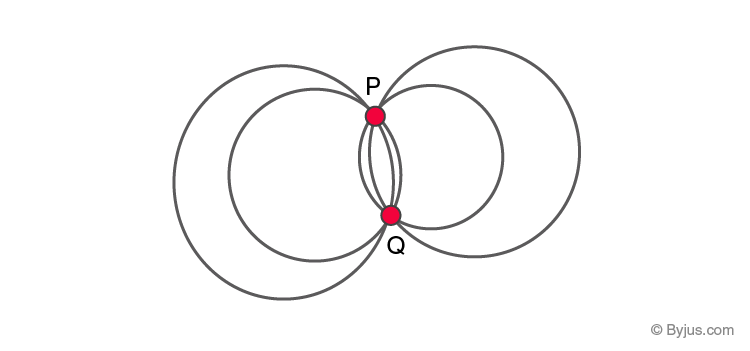
Once more nosotros see that an infinite number of circles passing through points P and Q can be drawn.

Circle Passing Through Three Points (Collinear or Not-Collinear)

Permit us now take 3 points. For a circumvolve passing through 3 points, 2 cases tin can arise.

• 3 points tin can exist collinear
• 3 points can be non-collinear

Let us report both cases individually.

Case 1: A circumvolve passing through 3 points: Points are collinear

Consider three points, P, Q and R, which are collinear.

If three points are collinear, any one of the points either prevarication outside the circle or inside it. Therefore, a circle passing through iii points, where the points are collinear, is not possible.

Case 2: A circumvolve passing through 3 points: Points are non-collinear

To draw a circle passing through three non-collinear points, nosotros need to locate the center of a circumvolve passing through 3 points and its radius. Follow the steps given below to sympathize how we tin can describe a circumvolve in this case.

Step i: Take 3 points P, Q, R and join the points as shown beneath:

Pace 2: Draw perpendicular bisectors of PQ and RQ. Permit the bisectors AB and CD meet at O such that the indicate O is chosen the centre of the circle.

Stride 3: Draw a circle with O as the centre and radius OP or OQ or OR. Nosotros get a circle passing through 3 points P, Q, and R.

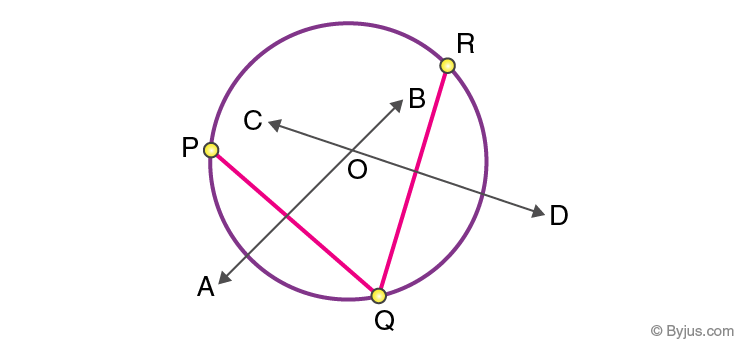
It is observed that only a unique circle will pass through all iii points. It tin can be stated equally a theorem and the proof is explained equally follows.

Information technology is observed that but a unique circle will pass through all three points. Information technology tin can be stated as a theorem, and the proof of this is explained below.

Given:

Three non-collinear points P, Q and R

To prove:

Only ane circumvolve can be drawn through P, Q and R

Construction:

Bring together PQ and QR.

Draw the perpendicular bisectors of PQ and QR such that these perpendiculars intersect each other at O.

Proof:

Southward. No	Statement	Reason
i	OP = OQ	Every betoken on the perpendicular bisector of a line segment is equidistant from the endpoints of the line segment.
2	OQ = OR	Every signal on the perpendicular bisector of a line segment is equidistant from the endpoints of the line segment.
3	OP = OQ = OR	From (i) and (two)
4	O is equidistant from P, Q and R

If a circumvolve is drawn with O as centre and OP as radius, then it volition also pass through Q and R.

O is the just betoken which is equidistant from P, Q and R as the perpendicular bisectors of PQ and QR intersect at O only.

Thus, O is the centre of the circumvolve to exist drawn.

OP, OQ and OR volition be radii of the circle.

From in a higher place information technology follows that a unique circle passing through 3 points can be fatigued given that the points are non-collinear.

Till now, you learned how to describe a circle passing through 3 not-collinear points. Now, you will larn how to find the equation of a circumvolve passing through 3 points . For this we need to take iii non-collinear points.

Circumvolve Equation Passing Through three Points

Let's derive the equation of the circle passing through the 3 points formula.

Permit P(x_i, y₁), Q(x₂, y_two) and R(x₃, y_three) be the coordinates of iii non-collinear points.

We know that,

The general form of equation of a circle is: x² + y² + 2gx + 2fy + c = 0….(1)

Now, we need to substitute the given points P, Q and R in this equation and simplify to get the value of g, f and c.

Substituting P(ten₁, y₁) in equ(1),

ten_ane ^two + y₁ ⁱⁱ + 2gx₁ + 2fy_ane + c = 0….(ii)

x₂ ^two + y₂ ⁱⁱ + 2gx_ii + 2fy₂ + c = 0….(3)

x₃ ² + y₃ ² + 2gx₃ + 2fy₃ + c = 0….(four)

From (ii) we become,

2gx_i = -x₁ ² – y₁ ² – 2fy₁ – c….(5)

Again from (2) we get,

c = -x₁ ² – y₁ ⁱⁱ – 2gx₁ – 2fy_i….(6)

From (4) we get,

2fy₃ = -ten₃ ² – y₃ ² – 2gx₃ – c….(7)

At present, subtracting (3) from (two),

2g(x₁ – 10₂) = (ten_two ⁱⁱ -x₁ ²) + (y_ii ² – y_ane ²) + 2f (y_two – y₁)….(viii)

Substituting (half dozen) in (vii),

2fy3 = -x₃ ² – y₃ ² – 2gx_three + 10₁ ² + y_i ⁱⁱ + 2gx_ane + 2fy₁….(9)

Now, substituting equ(eight), i.e. 2g in equ(9),

2f = [(x₁ ⁱⁱ – x₃ ⁱⁱ)(x₁ – ten₂) + (y₁ ² – y₃ ² )(x_one – x₂) + (x₂ ² – x₁ ⁱⁱ)(10₁ – x₃) + (y₂ ² – y₁ ²)(x₁ – 10₃)] / [(y_iii – y₁)(x₁ – x₂) – (y₂ – y₁)(x_ane – ten₃)]

Similarly, nosotros tin go 2g as:

2g = [(x₁ ² – x₃ ²)(y₁ – x_two) + (y_one ² – y₃ ²)(y₁ – y_ii) + (x_ii ² – x₁ ⁱⁱ)(y_i – y₃) + (y₂ ^two – y_i ²)(y_i – y₃)] / [(x₃ – ten₁)(y_ane – y₂) – (10₂ – x_ane)(y_i – y₃)]

Using these 2g and 2f values we can go the value of c.

Thus, by substituting g, f and c in (1) nosotros will get the equation of the circumvolve passing through the given three points.

Solved Example

Question:

What is the equation of the circumvolve passing through the points A(ii, 0), B(-2, 0) and C(0, two)?

Solution:

Consider the general equation of circle:

ten^two + y² + 2gx + 2fy + c = 0….(i)

Substituting A(ii, 0) in (i),

(2)² + (0)² + 2g(2) + 2f(0) + c = 0

iv + 4g + c = 0….(ii)

Substituting B(-two, 0) in (i),

(-2)² + (0)² + 2g(-2) + 2f(0) + c = 0

4 – 4g + c = 0….(iii)

Substituting C(0, ii) in (i),

(0)² + (ii)² + 2g(0) + 2f(2) + c = 0

4 + 4f + c = 0….(iv)

Adding (2) and (iii),

iv + 4g + c + 4 – 4g + c = 0

2c + 8 = 0

2c = -8

c = -4

Substituting c = -4 in (2),

four + 4g – 4 = 0

4g = 0

g = 0

Substituting c = -4 in (4),

4 + 4f – 4 = 0

4f = 0

f = 0

Now, substituting the values of m, f and c in (i),

x² + y^two + two(0)x + 2(0)y + (-4) = 0

x² + yⁱⁱ – 4 = 0

Or

x² + y² = iv

This is the equation of the circle passing through the given 3 points A, B and C.

To know more about the surface area of a circle, equation of a circumvolve, and its properties download BYJU'South-The Learning App.

hammcooncers.blogspot.com

Source: https://byjus.com/maths/circle-passing-through-3-points/

Share this post